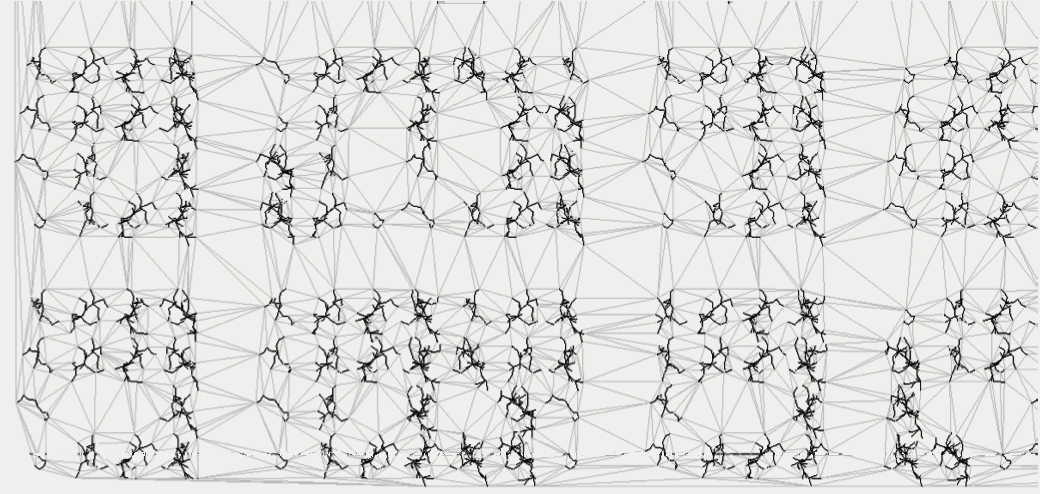
 nested rhythmic trees representation generated by jtol and visualized by rhino for 完璧な回
nested rhythmic trees representation generated by jtol and visualized by rhino for 完璧な回
— For the latest version : download jtol from github.
Jtol is built and used by jt rinker and olivier pasquet. It is a HUGE library dedicated to real-time pattern generation and can be applied to architectural design, music, dance; everything requiring constructed evolution in space and time.
It deals with multi-scaling and multi-dimensions where rhythm is considered to be a skeleton onto everything else is attached (pitches, params…).
Jtol was first programmed in python in max with the help of bertrand nouvel. It gathered data structures similar to the jitter library but with a nested architecture.
A newer version is now using the bach library and still runs in max. It has nevertheless been programmed in order to always be able to easily get rid of the bach library. It is inspired by libraries like athenaCL, numpy, scipy, abjad, pyevolve, pwgl and open music. Some purely generative music devices will soon come for max for live. Releases are laborious; so feel free to use it and debug it.
Here are some possible interests for jtol:
| ENP-like notation in max, nested tree system for rhythm |
| beat repetitions, looped based generators |
| braid theory, tessellation |
| cellular automata and multi-agent systems |
| chaos |
| sieves |
| permutative, serial functions |
| multi-order markov chains |
| multi-set |
| quantization, interpolation and extrapolation |
| pitch functions |
| genetic algorithms |
____________________________________________________________________________________________________________________________________
EXAMPLES
+++ jtol.bach.ratio
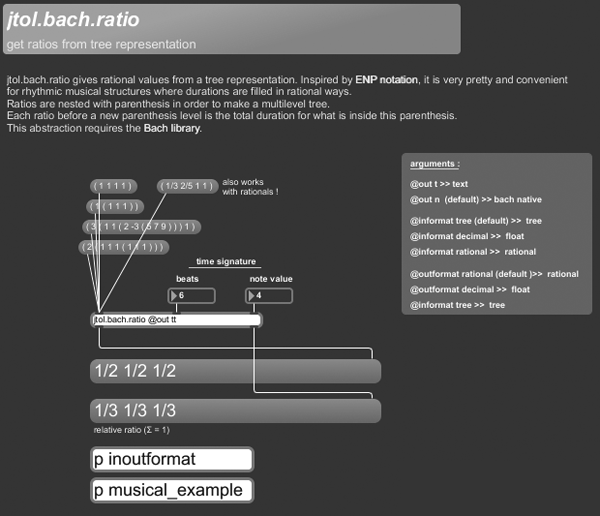
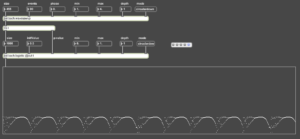
jtol.bach.ratio gives rational values from a tree representation. Inspired by ENP notation, it is very pretty and convenient for rhythmic musical structures where durations are filled in rational ways.
Ratios are nested with parenthesis in order to make a multilevel tree.
Each ratio before a new parenthesis level is the total duration for what is inside this parenthesis.
For instance, simple musical tuplets would be expressed this way:
• ( 1 ( 1 1 1 ) ) => ( 1/3 1/3 1/3 ) => ( 0.333 0.333 0.333 ) (Σ 1)
• ( 1 ( 1 1 ( 1 1 1 ) ) ) => ( 1/2 1/6 1/6 1/6 ) => ( 0.5 0.1667 0.1667 0.1667 ) (Σ 1)
There is a very close relation with spatial tessellations like voronoi‘s one where the delaunay triangulation would be practical.
____________________________________________________________________________________________________________________________________
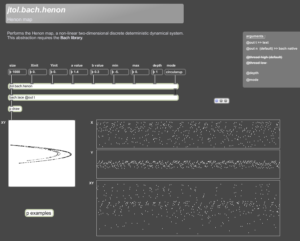
+++ jtol.bach.henon
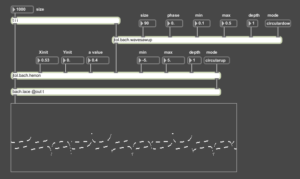
jtol.bach.henon is one of the available generators. As an example, this one performs the henon map, a non-linear two-dimensional discrete deterministic dynamical system.
For most generators, each parameter can be a scalar, a vector or a tree. This allows a cell-by-cell and a step-by-step control for the generated forms.
 |
 |
____________________________________________________________________________________________________________________________________
+++ jtol.bach.play
jtol.bach.play converts ratios from jtol.bach2score to millisecond timings and outputs corresponding time-delayed bangs when a ‘play’ message is received.
____________________________________________________________________________________________________________________________________
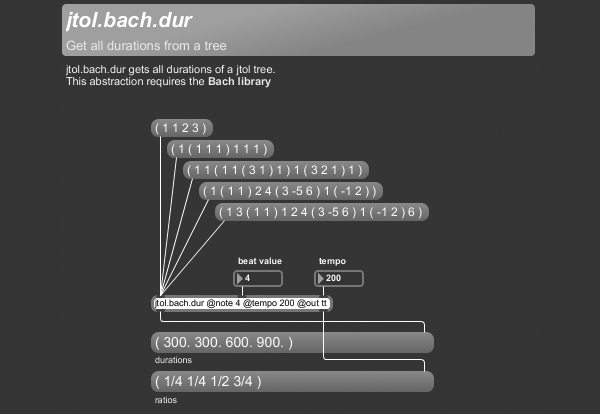
+++ jtol.bach.dur
jtol.bach.dur gets all durations of a jtol tree.
____________________________________________________________________________________________________________________________________
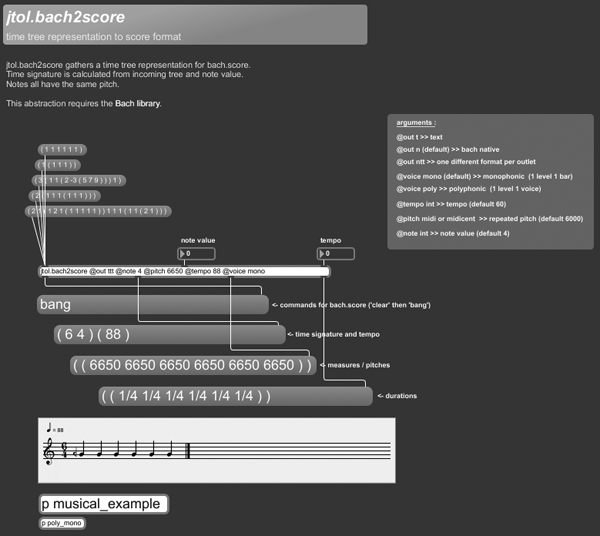
+++ jtol.bach.2score
jtol.bach2score gathers a time tree representation for bach.score. Time signature is calculated from incoming tree and note value.
____________________________________________________________________________________________________________________________________
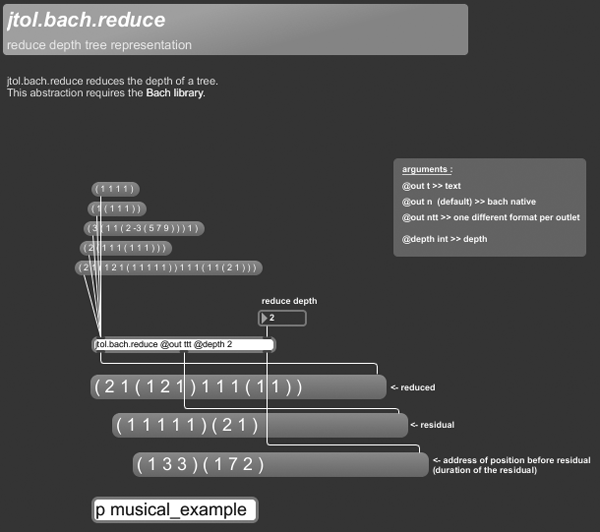
+++ jtol.bach.reduce
jtol.bach.reduce reduces the depth of trees. For instance, if we have the following tree:
( 2 1 ( 1 2 1 ( 1 1 ( 1 1 1 ) ) ) 1 1 1 ( 1 1 ( 2 1 ) ) )
=> ( 2 1 ( 1 2 1 ( 1 1 ) ) 1 1 1 ( 1 1 ) )
=> ( 2 1 ( 1 2 1 ) 1 1 1 )
=> ( 2 1 1 1 1 )
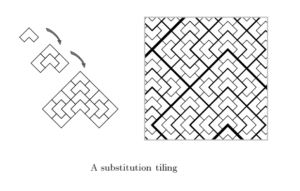
A reduction of deepness is very convenient for playing with the degree of complexity of a rhythm. Questions relative to tempo and scale similarity (starting point for fractals) rise from this process. Nevertheless, it is a question of tiling.
Raphael Robinson wrote an interesting paper about aperiodical hierarchical tilings in 1996.
____________________________________________________________________________________________________________________________________
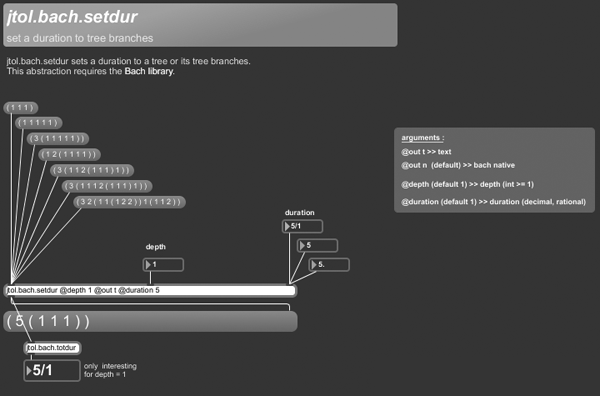
+++ jtol.bach.setdur
jtol.bach.setdur sets a duration to a tree or its tree branches.
____________________________________________________________________________________________________________________________________
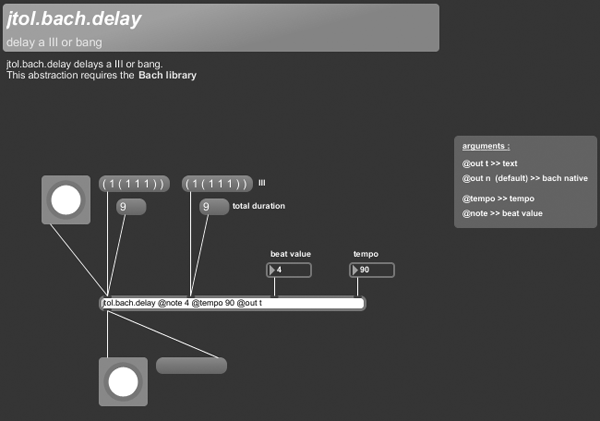
+++ jtol.bach.delay
jtol.bach.delay delays a III or bang.
____________________________________________________________________________________________________________________________________
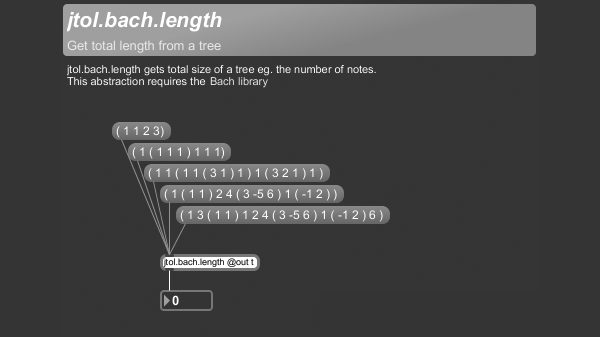
+++ jtol.bach.length
jtol.bach.length gets total size of a tree eg. the number of notes.
____________________________________________________________________________________________________________________________________
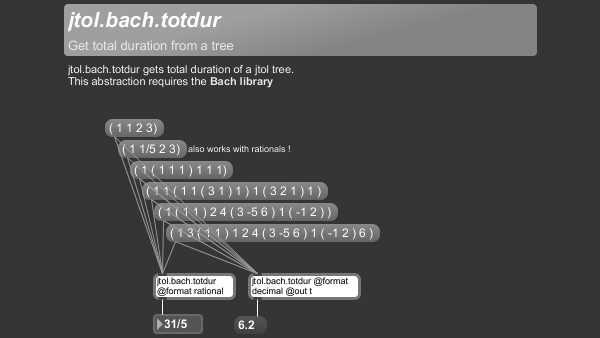
+++ jtol.bach.totdur
jtol.bach.totdur gets total duration of a jtol tree.
____________________________________________________________________________________________________________________________________
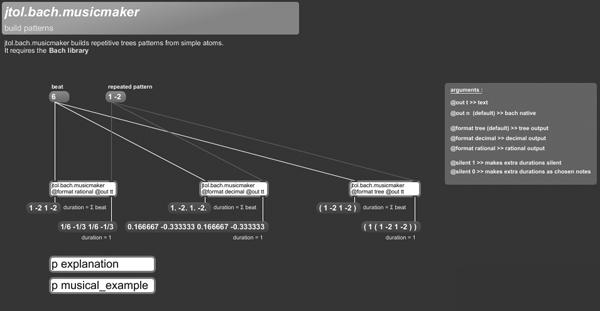
+++ jtol.bach.musicmaker
jtol.bach.musicmaker builds repetitive trees patterns from simple atoms. Inspired by Sébastien Gaxie OM patch.
____________________________________________________________________________________________________________________________________
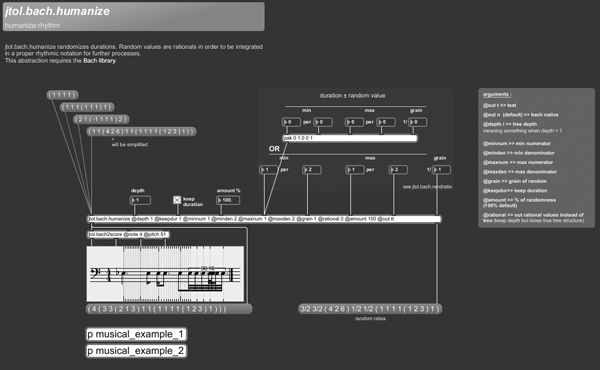
+++ jtol.bach.humanize
jtol.bach.humanize randomizes durations. Random values are rationals in order to be integrated in a proper rhythmic notation for further processes.
____________________________________________________________________________________________________________________________________
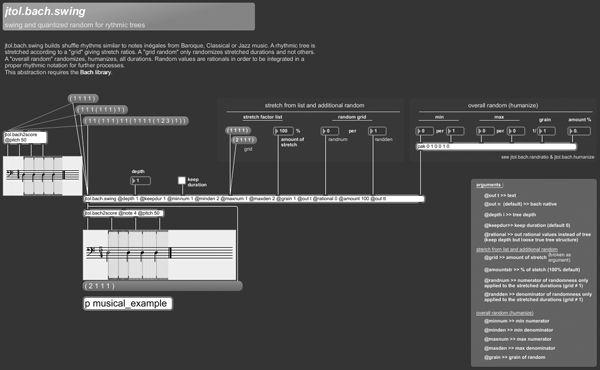
+++ jtol.bach.swing
jtol.bach.swing builds shuffle rhythms similar to notes inégales from Baroque, Classical or Jazz music. A rhythmic tree is stretched according to a “grid” giving stretch ratios. A “grid random” only randomizes stretched durations and not others. A “overall random” randomizes, humanizes, all durations. Random values are rationals in order to be integrated in a proper rhythmic notation for further processes.
____________________________________________________________________________________________________________________________________
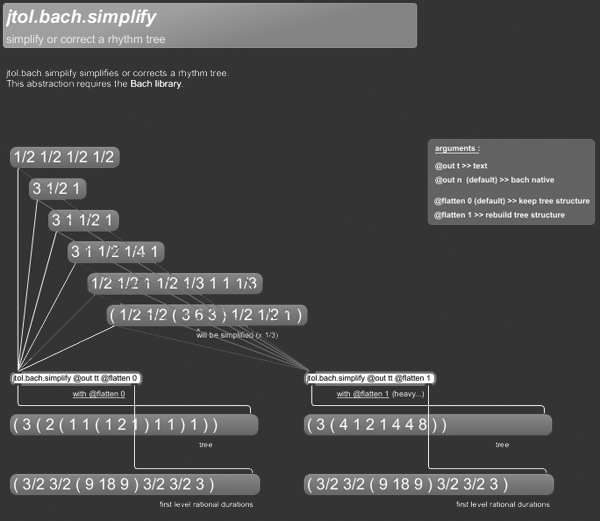
+++ jtol.bach.simplify
jtol.bach.simplify simplifies or corrects a rhythm tree.
____________________________________________________________________________________________________________________________________
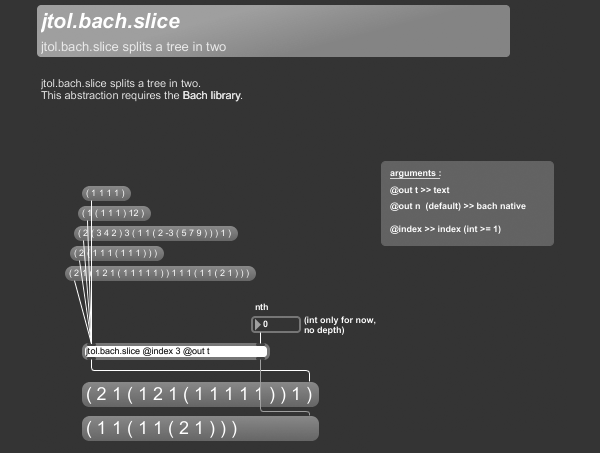
+++ jtol.bach.slice
jtol.bach.slice splits a tree in two.
____________________________________________________________________________________________________________________________________
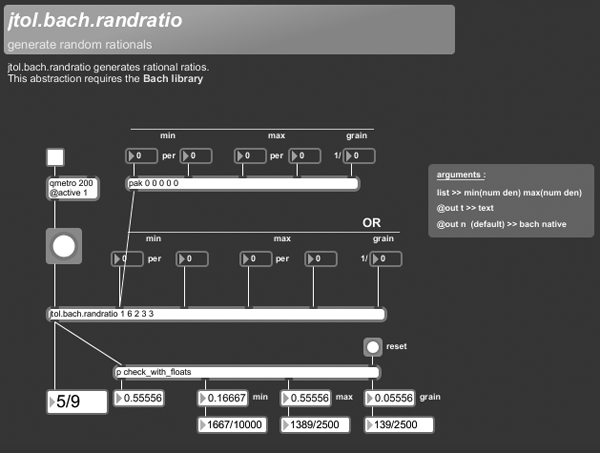
+++ jtol.bach.randratio
jtol.bach.randratio generates rational ratios.
____________________________________________________________________________________________________________________________________
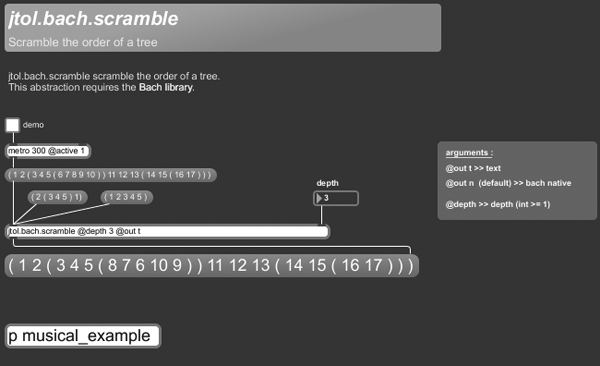
+++ jtol.bach.scramble
jtol.bach.scramble scramble the order of a tree.
____________________________________________________________________________________________________________________________________
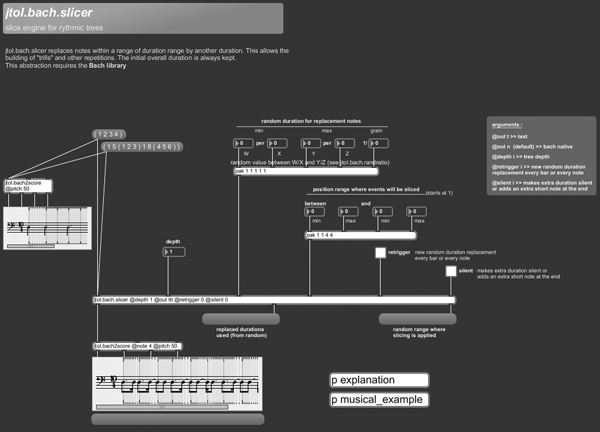
+++ jtol.bach.slicer
jtol.bach.slicer replaces notes within a range of duration range by another duration. This allows the building of “trills” and other repetitions. The initial overall duration is always kept.
____________________________________________________________________________________________________________________________________
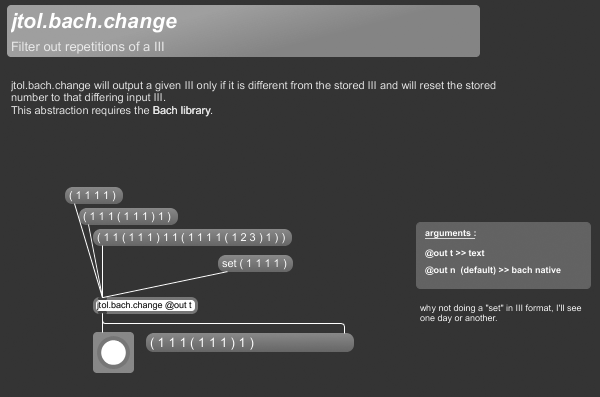
+++ jtol.bach.change
jtol.bach.change will output a given III only if it is different from the stored III and will reset the stored number to that differing input III.
____________________________________________________________________________________________________________________________________
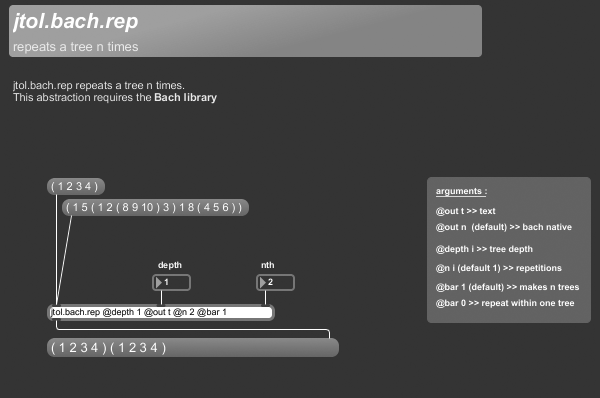
+++ jtol.bach.rep
jtol.bach.rep repeats a tree n times.
____________________________________________________________________________________________________________________________________
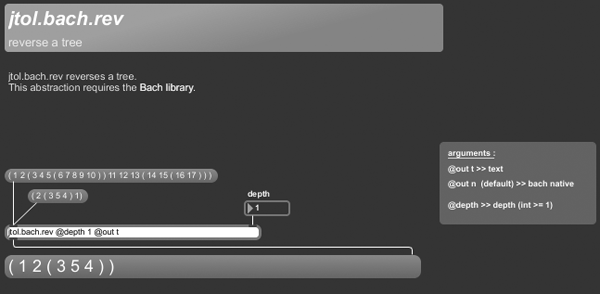
+++ jtol.bach.rev
jtol.bach.rev reverses a tree.
____________________________________________________________________________________________________________________________________
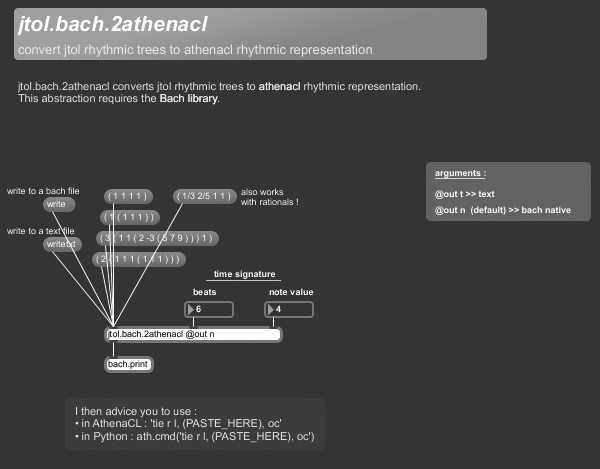
+++ jtol.bach.2athenacl
jtol.bach.2athenacl converts jtol rhythmic trees to athenaCL rhythmic representation.
____________________________________________________________________________________________________________________________________
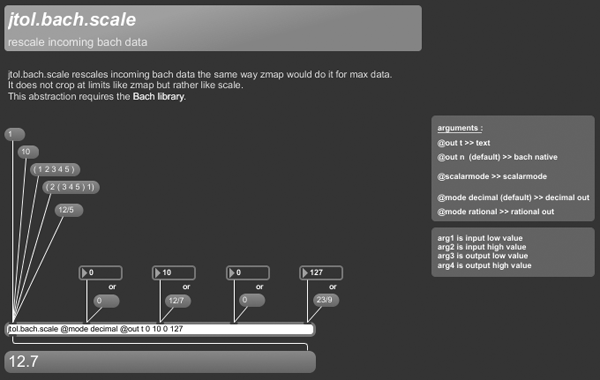
+++ jtol.bach.scale
jtol.bach.scale rescales incoming bach data the same way zmap would do it for max data.
It does not crop at limits like zmap but rather like scale.
____________________________________________________________________________________________________________________________________
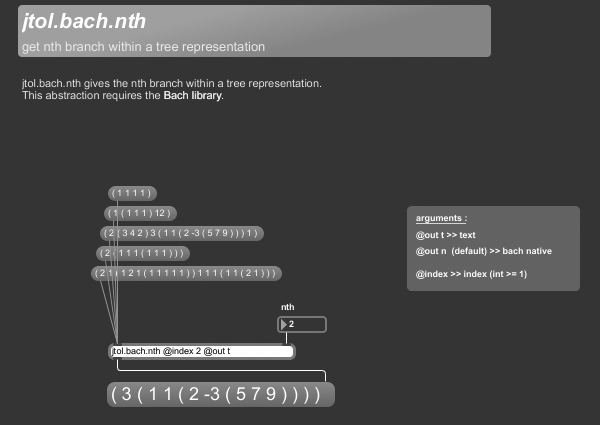
+++ jtol.bach.nth
jtol.bach.nth gives the nth branch within a tree representation.
____________________________________________________________________________________________________________________________________
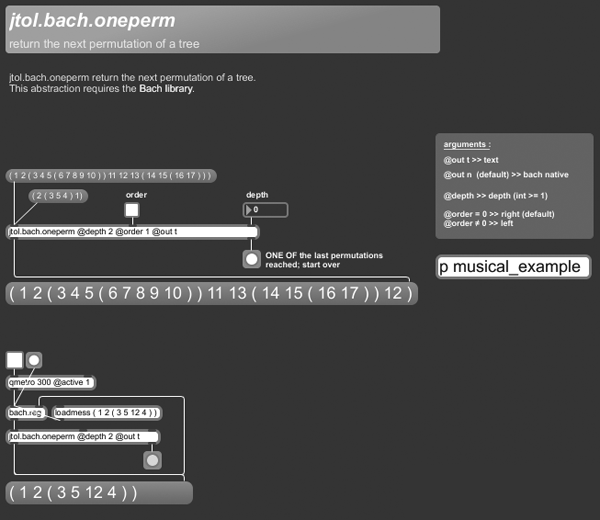
+++ jtol.bach.oneperm
jtol.bach.oneperm return the next permutation of a tree.
____________________________________________________________________________________________________________________________________
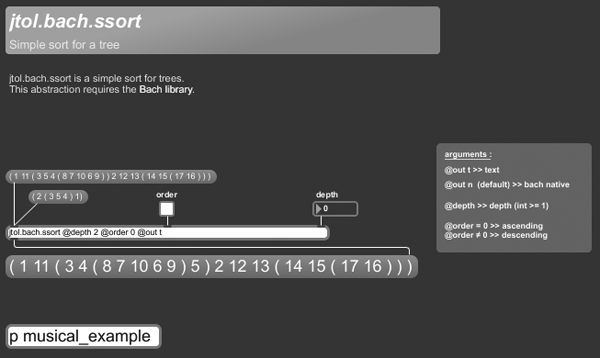
+++ jtol.bach.ssort
jtol.bach.ssort is a simple sort for trees.
____________________________________________________________________________________________________________________________________
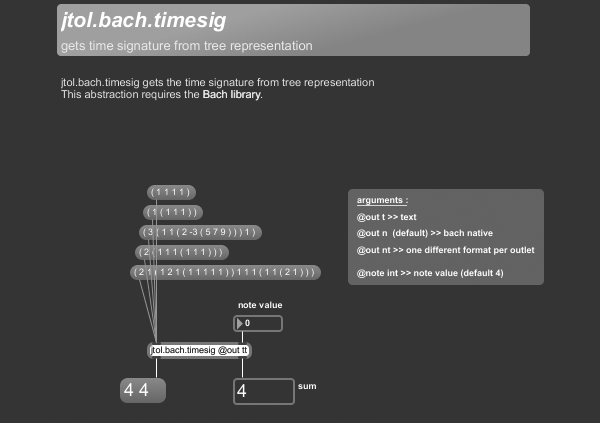
+++ jtol.bach.timesig
jtol.bach.timesig gets the time signature from tree representation.
____________________________________________________________________________________________________________________________________
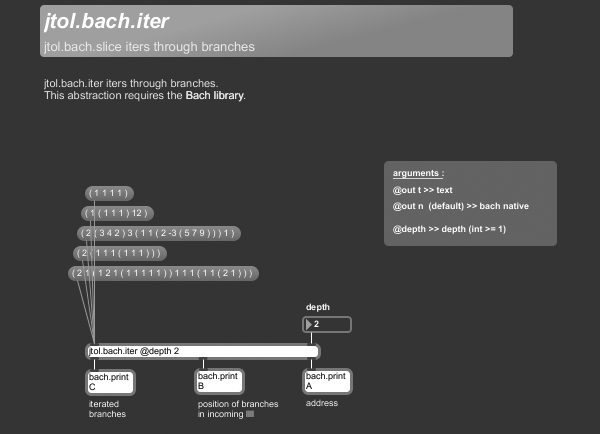
+++ jtol.bach.iter
jtol.bach.iter iters through branches.
____________________________________________________________________________________________________________________________________
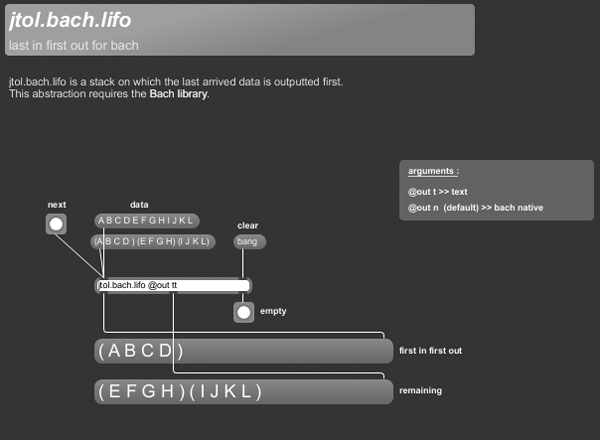
+++ jtol.bach.lifo
jtol.bach.lifo is a stack on which the last arrived data is outputted first.
____________________________________________________________________________________________________________________________________
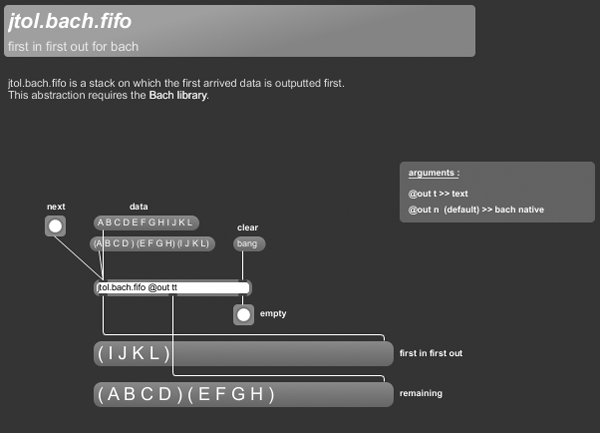
+++ jtol.bach.fifo
jtol.bach.fifo is a stack on which the first arrived data is outputted first.
____________________________________________________________________________________________________________________________________
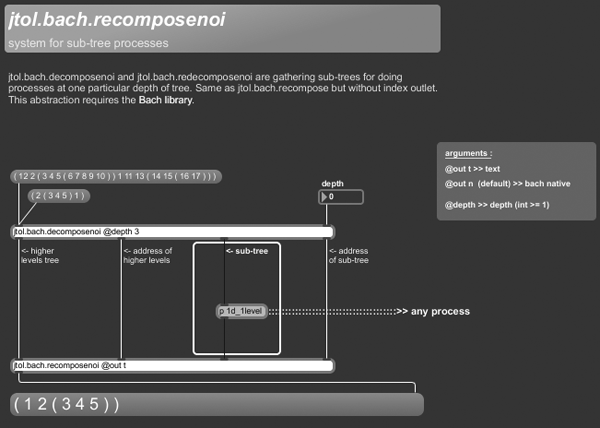
+++ jtol.bach.decomposenoi
jtol.bach.decomposenoi and jtol.bach.redecomposenoi are gathering sub-trees for doing processes at one particular depth of tree. Same as jtol.bach.recompose but without index outlet.
____________________________________________________________________________________________________________________________________
+++ jtol.bach.recomposenoi
jtol.bach.decomposenoi and jtol.bach.redecomposenoi are gathering sub-trees for doing processes at one particular depth of tree. Same as jtol.bach.recompose but without index outlet.